
Zadanie Punkty (pun)
Pomóż nam usprawnić bazę zadań!
Punkty
Limit pamięci: 64 MB
Mamy dane 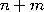 punktów na płaszczyźnie. Wśród nich jest dokładnie
punktów na płaszczyźnie. Wśród nich jest dokładnie  punktów białych i
punktów białych i 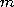 punktów czarnych.
Twoim zadaniem jest policzenie liczby trójkątów o wierzchołkach w białych punktach,
które nie zawierają w sobie żadnego czarnego punktu.
punktów czarnych.
Twoim zadaniem jest policzenie liczby trójkątów o wierzchołkach w białych punktach,
które nie zawierają w sobie żadnego czarnego punktu.
Można założyć, że żadne trzy punkty nie są współliniowe.
Wejście
Pierwszy wiersz wejścia zawiera dwie liczby całkowite  i
i 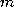 (
(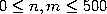 ), oznaczające
odpowiednio liczbę białych oraz czarnych punktów.
), oznaczające
odpowiednio liczbę białych oraz czarnych punktów.
Kolejne  wierszy zawiera opisy białych punktów, a następne
wierszy zawiera opisy białych punktów, a następne 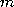 wierszy opisy punktów czarnych.
Każdy wiersz zawiera dwie liczby całkowite
wierszy opisy punktów czarnych.
Każdy wiersz zawiera dwie liczby całkowite  i
i 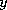 (
(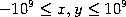 ),
oznaczające współrzędne punktu.
),
oznaczające współrzędne punktu.
Możesz założyć, że w testach wartych łącznie 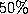 punktów zachodzą dodatkowe warunki
punktów zachodzą dodatkowe warunki 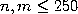 ,
a w testach wartych łącznie
,
a w testach wartych łącznie 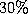 punktów zachodzi
punktów zachodzi 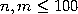 .
.
Wyjście
Pierwszy wiersz wyjścia powinien zawierać jedną liczbę całkowitą, równą liczbie trójkątów o wierzchołkach w białych punktach, które nie zawierają w sobie żadnego czarnego punktu.
Przykład
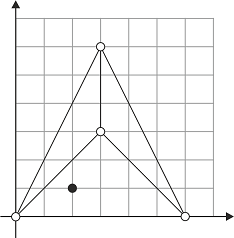
Dla danych wejściowych:
4 1 6 0 3 6 3 3 0 0 2 1
poprawną odpowiedzią jest:
2
Autor zadania: Mateusz Litwin (zapożyczenie).
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English